Why Have Embedding Models Stagnated?

October 2024 marked a subtle milestone in AI development: an entire quarter passed without a single fundamental architectural innovation in text embedding models. New models were released—Voyage AI updated benchmarks, OpenAI tweaked pricing, Cohere announced dimension flexibility. But beneath the noise, every "new" model was just a better-trained version of the same transformer architecture we've been using since BERT.

The field of embedding models is experiencing something rare in modern AI: genuine maturity. Performance improvements have decelerated from 1.4% monthly gains in 2022-2023 to 0.1-0.2% monthly in 2024-2025. The top seven models on MTEB (Massive Text Embedding Benchmark—the industry standard leaderboard) cluster within 4 points of each other.

This slowdown isn't for lack of imagination or investment. I will make the argument that it is the natural consequence of approaching fundamental mathematical limits inherent to the single-vector embedding paradigm.

Embedding Boom Times: 2018-2022

To contextualize the stagnation, it is important to realize just how rapid the innovations were at one point. The period from 2018 to 2022 witnessed paradigm shifts so fundamental they redefined how machines understand language and meaning

October 2018: BERT Arrives

Google's BERT represented the first true evolution. Prior approaches like Word2Vec and GloVe treated words as static entities, for example, "bank" always meant the same thing regardless of whether you were discussing rivers or finance. BERT introduced deeply bidirectional transformers that generated contextual representations, where every word's embedding depended on its entire surrounding context.

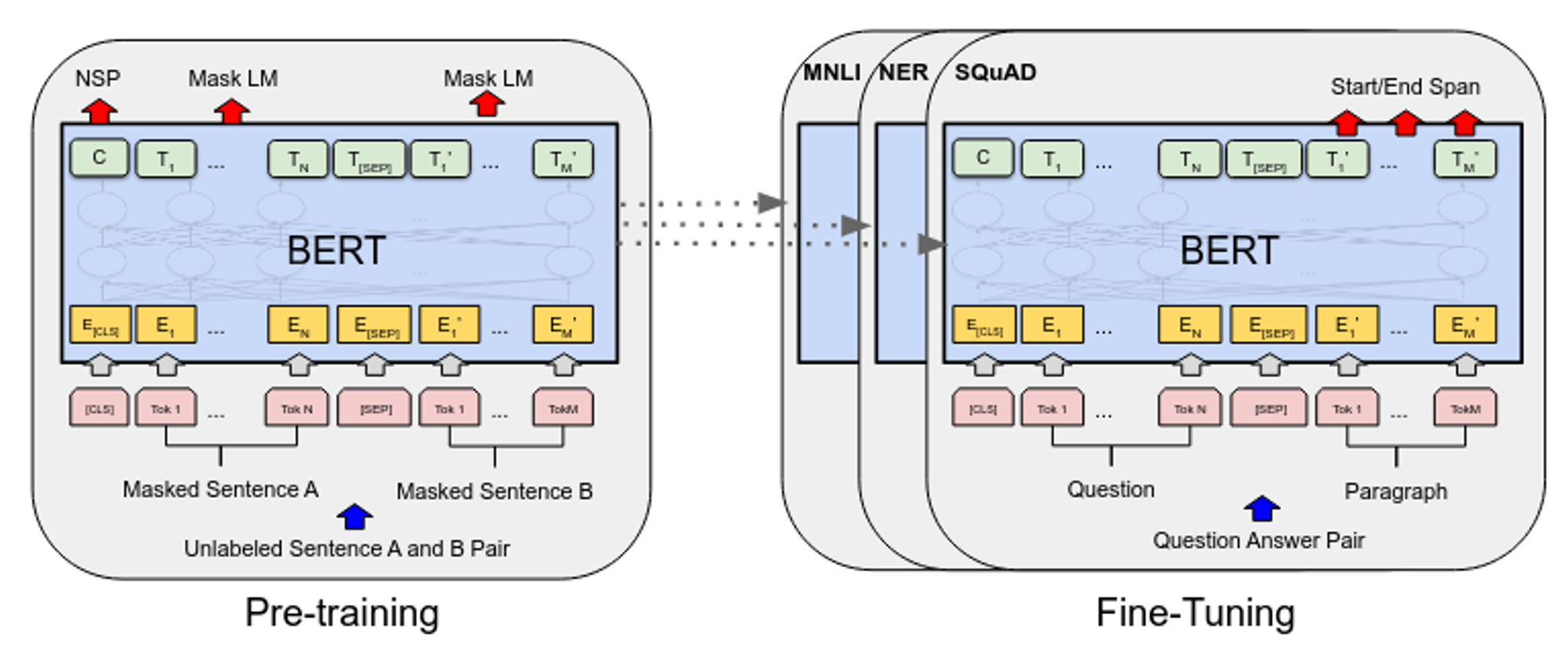
The architecture was elegant: 12 transformer layers (110M parameters for BERT-base) trained on masked language modeling and next sentence prediction. Given a sentence with masked tokens, BERT learned to predict them using bidirectional context—a task that forced the model to develop rich semantic understanding. This enabled transfer learning across diverse language tasks through a single pre-trained model.

But BERT had a crippling limitation: sentence-level embeddings were terrible! Computing semantic similarity between two sentences required quadratic comparisons such that finding similar sentences in a 10,000-document corpus took 65 hours on a V100 GPU.

August 2019: Sentence-BERT Unlocks Practical Retrieval

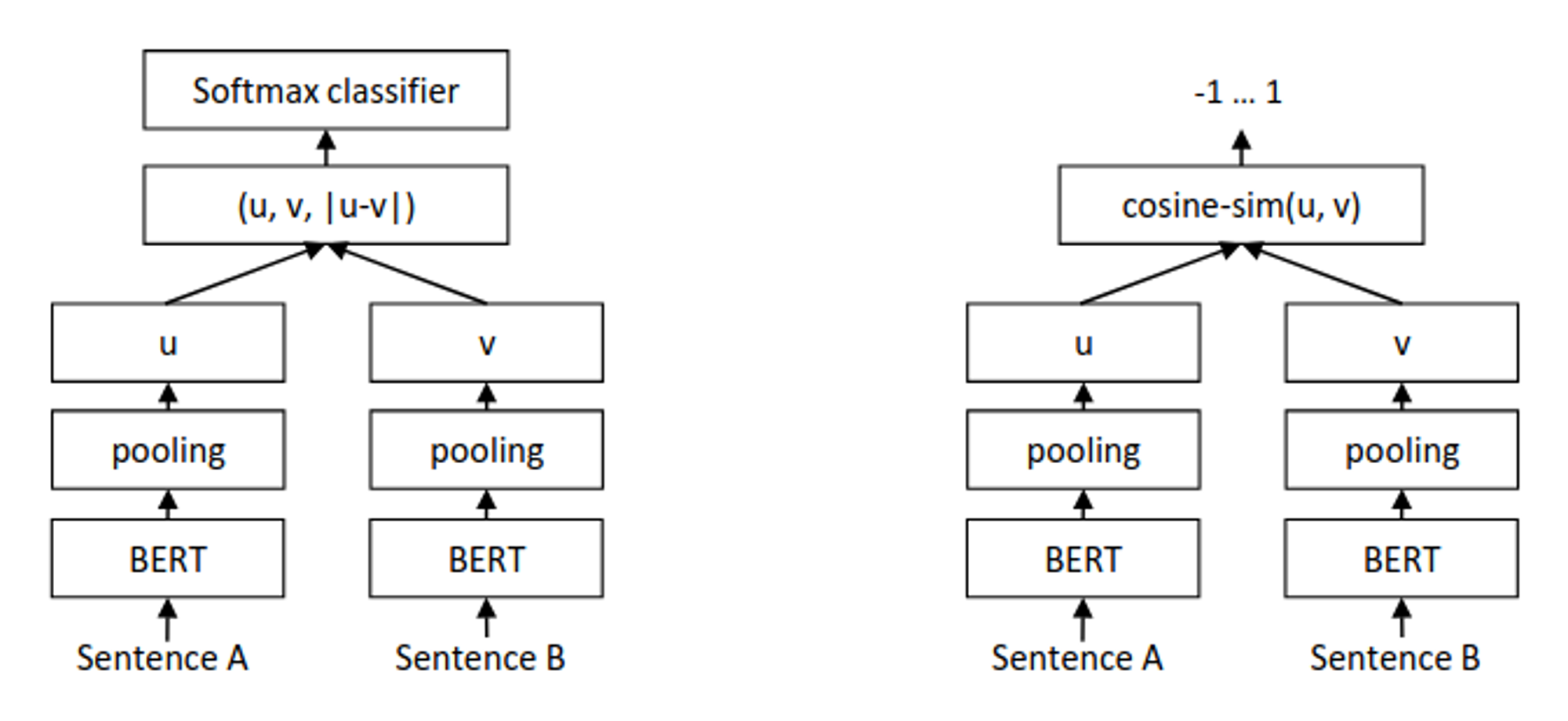
Nils Reimers and Iryna Gurevych solved this bottleneck with a deceptively simple architectural modification. Sentence-BERT employed siamese networks: two identical BERT models processing sentences independently, with their outputs pooled into fixed-length vectors. The transformation was incredibly impressive- semantic search between 10,000 sentences dropped from 65 hours to 5 seconds—a 46,800x speedup. This single change made semantic search viable and gave rise to the sentence-transformers library that underpins most modern search systems.

Mathematical Foundations: Where Theory Binds Practice

Now to understand why innovation has stalled, we must examine the mathematics that simultaneously enables and constrains current approaches.

Contrastive Learning and InfoNCE: The Information-Theoretic View

Here's the core insight that made modern embeddings work: you want embeddings where similar things are close together and different things are far apart. Simple enough. But how do you actually train that into a neural network?

The breakthrough was contrastive learning, and specifically an objective function called InfoNCE (Noise Contrastive Estimation). Here's what it does in practice: show the model a query and a relevant document (positive pair), then show it the same query with a bunch of irrelevant documents (negatives). The model learns to push the positive pair closer while pushing away the negatives.

The power of contrastive learning stems from a deep connection to information theory. Given a context vector c and positive target x+, we want representations that maximize their mutual information I(x+;c). The InfoNCE (Noise Contrastive Estimation) loss provides a tractable lower bound:

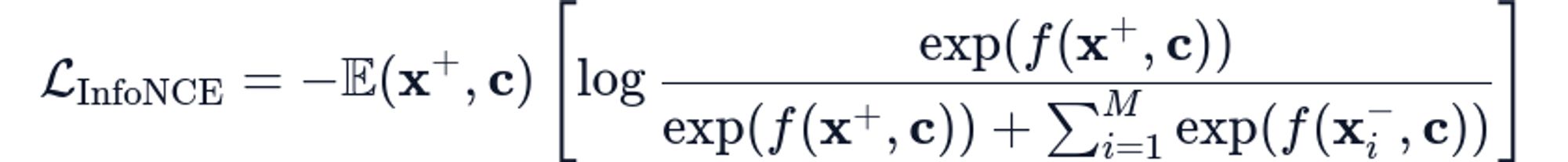
The theoretical guarantee is that as the number of negatives goes from M→∞, the loss provides a tight lower bound on mutual information:

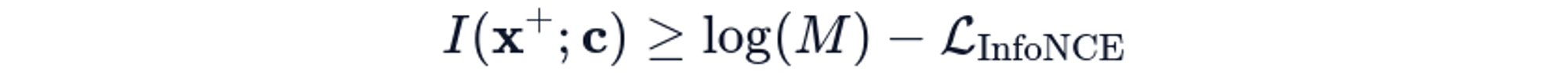
This connection is why contrastive learning works: by minimizing InfoNCE loss with many negatives, we're provably maximizing the mutual information between inputs and their representations.

Alignment and Uniformity: The Geometric Decomposition

Wang and Isola's 2020 analysis provided even deeper insight by decomposing contrastive learning into two geometric objectives. On the unit hypersphere, good embeddings must:

1. Align: Measure how close positive pairs are and pull these pairs close together
2. Be Uniform: Measure how evenly features are spread across the sphere

Too much alignment without uniformity leads to dimensional collapse– AKA all embeddings clumping in a small region. Too much uniformity without alignment loses semantic meaning.

This geometric view explains why contrastive learning represents a kind of optimum for single-vector embeddings. Any representation learning objective that doesn't balance alignment and uniformity will either lose semantic information or collapse to low-dimensional subspaces!

Dimensional Collapse: The Subspace Trap

Here's a weird problem: you train a model with 1024-dimensional embeddings, expecting to use all 1024 dimensions to encode rich information about your documents. Instead, the model secretly decides to use only 100-200 dimensions and leaves the rest mostly empty. Why?

Despite embedding spaces with hundreds or thousands of dimensions, learned representations often occupy surprisingly low-rank subspaces. Jing et al.'s 2022 analysis identified two mechanisms causing this phenomenon.

Augmentation-Induced Collapse: If augmentation adds noise with variance σ_aug^2 larger than the data variance σ_data^2 in some direction v, the model learns to suppress that direction entirely. Formally, for weight matrix W:

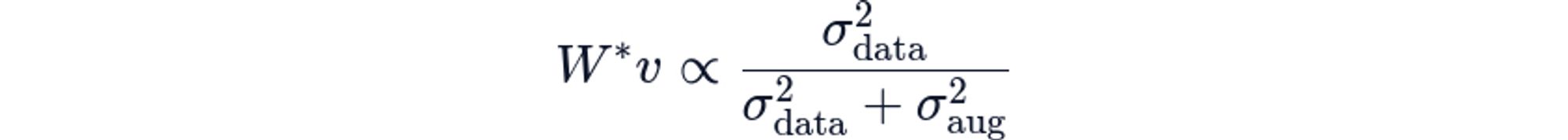
As augmentation variance dominates, W*v→0, eliminates that dimension from the representation. So, strong augmentation—once believed necessary for good contrastive learning—actually destroys representational capacity!

Think about it: if you randomly paraphrase sentences during training (a common augmentation), the model learns those paraphrases should have identical embeddings. To achieve this, it has to ignore anything that varies between paraphrases—which ends up being a lot of information.

Implicit Regularization: Neural networks trained with gradient descent exhibit implicit bias toward low-rank solutions, so for overparameterized networks, the gradient flow naturally reduces the effective rank of learned representations:

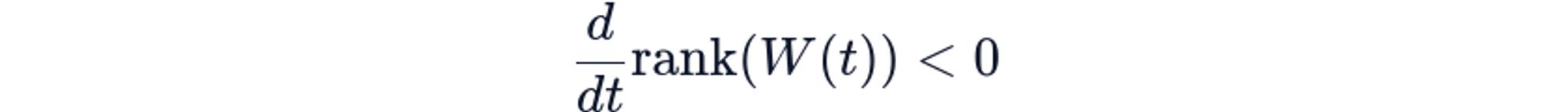
This isn't a bug; it's actually a fundamental property of overparameterized optimization. Flatter minima generalize better, and flatter minima have lower rank. So even with 1024-dimensional embeddings, effective dimensionality often drops to 100-200. In other words, the model doesn't use its full capacity. This places a hard limit on how much information single vectors can encode, regardless of nominal dimensionality.

The Sign-Rank Constraint: Geometric Impossibility

And now we are approaching the real limits to single-vector embedding. In recent theoretical work by Weller et al. (2025), they proved that single-vector embeddings face geometric impossibility constraints related to the sign-rank of query-relevance matrices.

To break this down a bit, imagine you have 1000 documents and 100 queries. For each query, some subset of documents is relevant. The question is: can you arrange these documents as points in space such that for every query, you can draw a flat plane that separates relevant documents from irrelevant ones?

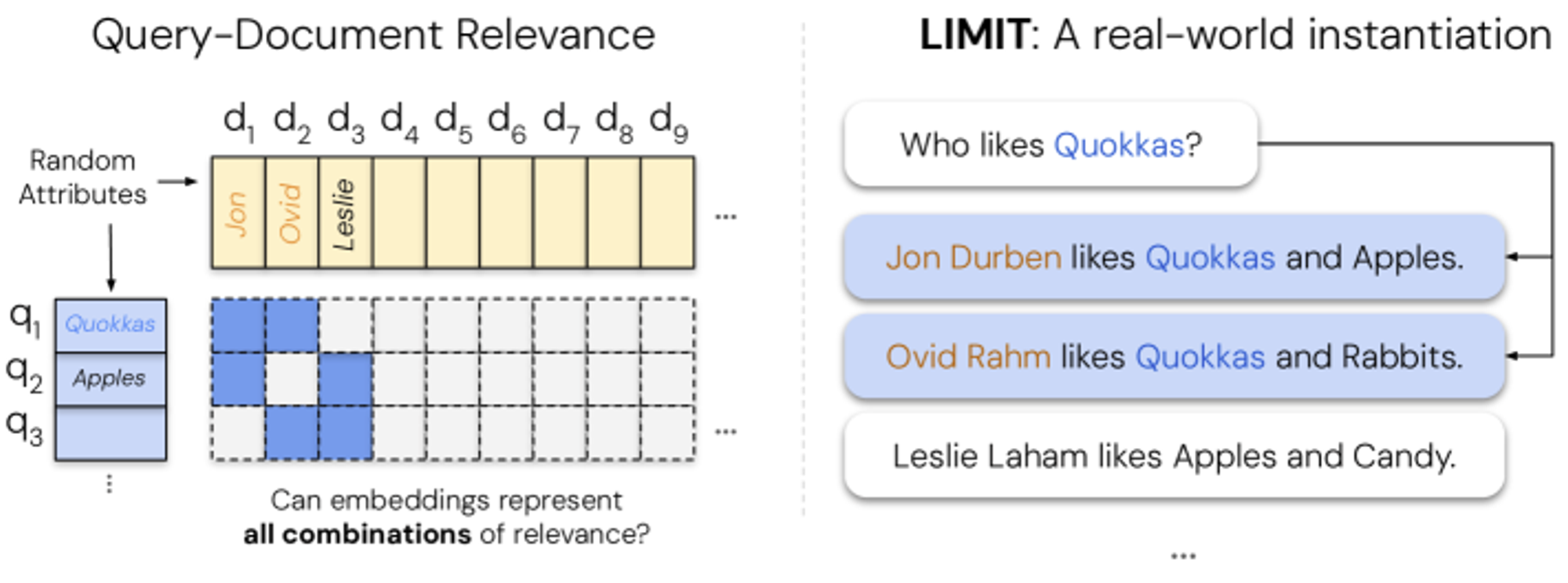
The answer, it turns out, is often “no”. And this is not a training problem or an architecture problem - it is a geometric impossibility. Consider a corpus of n documents and m queries. Define the relevance matrix: R{0,1}mn

Embedding-based retrieval using dot products can perfectly rank documents only if rank_土(R) ≤ d, where d is the embedding dimension and rank_土(R) is the sign-rank (the minimum dimension needed to write R=sign(UV^T) for matrices (U, V)).

If the sign-rank of your relevance matrix is higher than your embedding dimension, perfect retrieval is geometrically impossible. You literally cannot arrange the points in space to satisfy all your relevance judgements simultaneously. It is like trying to solve an overconstrained set of equations– no solution exists.

So now you might see the catch-22: you need high dimensions to escape sign-rank constraints, but neural networks collapse to low-rank subspaces regardless of nominal dimension. Single vector embeddings are mathematically trapped!

Alternative Paradigms: How we Escape the Single-Vector Problem

Recognition of single-vector limitations has some really interesting and novel approaches that may just represent the next paradigm shift.

ColBERT: Late Interaction and Multi-Vector Representations

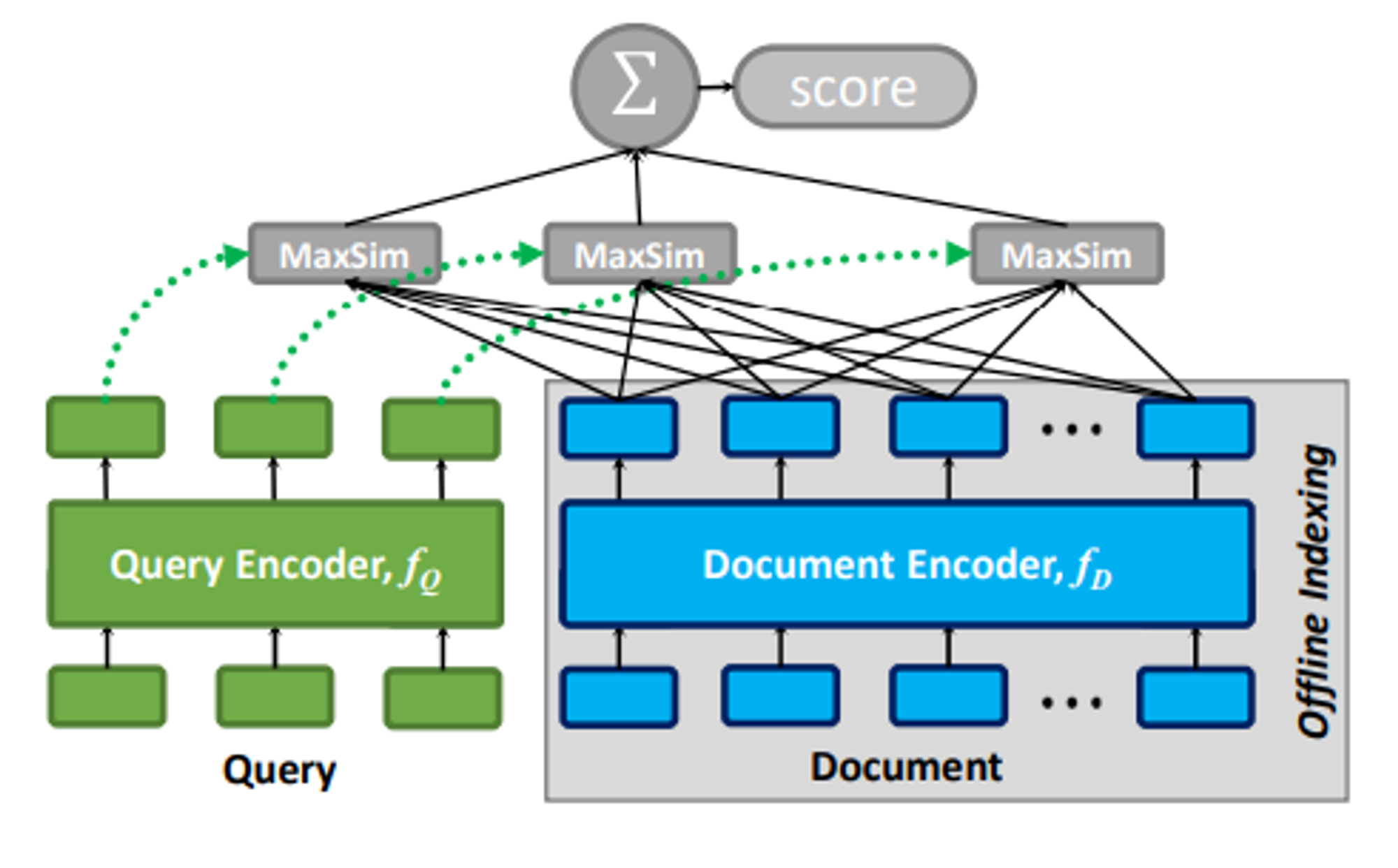
ColBERT (Contextualized Late Interaction over BERT) stores embeddings for each token rather than pooling to a single vector. During retrieval, it computes similarity through MaxSim operations: for each query token, compute maximum similarity across all document tokens, then sum:

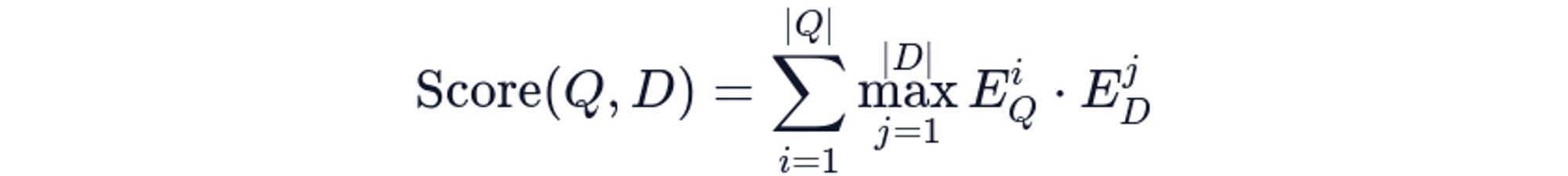
Where EQi is the embedding of query token i and EDj is the embedding of document token j. This late interaction preserves token-level nuances that single-vector approaches destroy through premature pooling.

The theoretical advantage is that multi-vector representations escape sign-rank constraints. A document with 100 tokens and 128-dimensional token embeddings effectively operates in a 12,800-dimensional space (though structured). This higher effective dimensionality allows representing complex relevance patterns that single vectors geometrically cannot.

Why hasn’t this received widespread adoption? Well, supporting token-level embeddings requires different indexing strategies, different storage layouts, and different query engines. The ecosystem hasn't caught up to the architecture… Yet.

SPLADE: Sparse Neural Retrieval

SPLADE (Sparse Lexical and Expansion Model) takes an orthogonal approach: neural models predict sparse representations over vocabulary terms. It uses BERT's masked language model head to predict term weights, performing learned term expansion while maintaining sparsity:

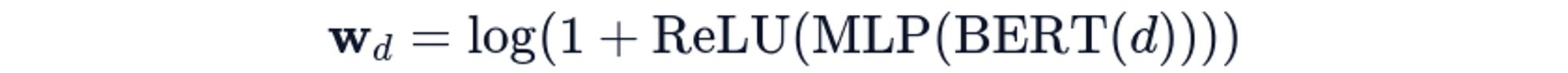
where each document d produces a sparse weight vector wd over the vocabulary (typically 30K terms). Most weights are zero; non-zero weights indicate both original terms and semantically related expansions.

The dual objectives are: maximize lexical recall through term expansion (query "ML model" retrieves documents about "machine learning algorithm") and minimize sparsity (regularize toward few non-zero terms for efficiency).

Sparse representations avoid single-vector information bottlenecks while enabling inverted index infrastructure. Traditional IR systems built for BM25 work with SPLADE, requiring no new vector databases. Performance gains of 9%+ NDCG@10 (Normalized Discounted Cumulative Gain at rank 10, a standard ranking quality metric) on TREC DL 2019 demonstrate viability.

So again, why hasn't SPLADE dominated? Same answer as ColBERT– infrastructural inertia.

How Sylow Approaches The Problem.

At Sylow, we build retrieval systems around the premise that single-vector approaches have matured and further gains require architectural diversity. Industry consensus has coalesced around multi-stage pipelines: fast dense retrieval (1M documents → 100), sparse or late interaction refinement (100 → 20), full reranking (20 → 5). The theoretical justification is sound—sparse methods excel at exact matching, dense methods capture semantic similarity, late interaction preserves token-level nuances. Each stage addresses the previous stage's limitations.

The challenge is complexity. Hybrid architectures require orchestrating multiple retrieval methods, tuning stage-specific weights, maintaining heterogeneous indexes, and reconciling disagreements between methods. This complexity barrier explains why most production systems default to single-vector dense embeddings despite measurable quality gaps.

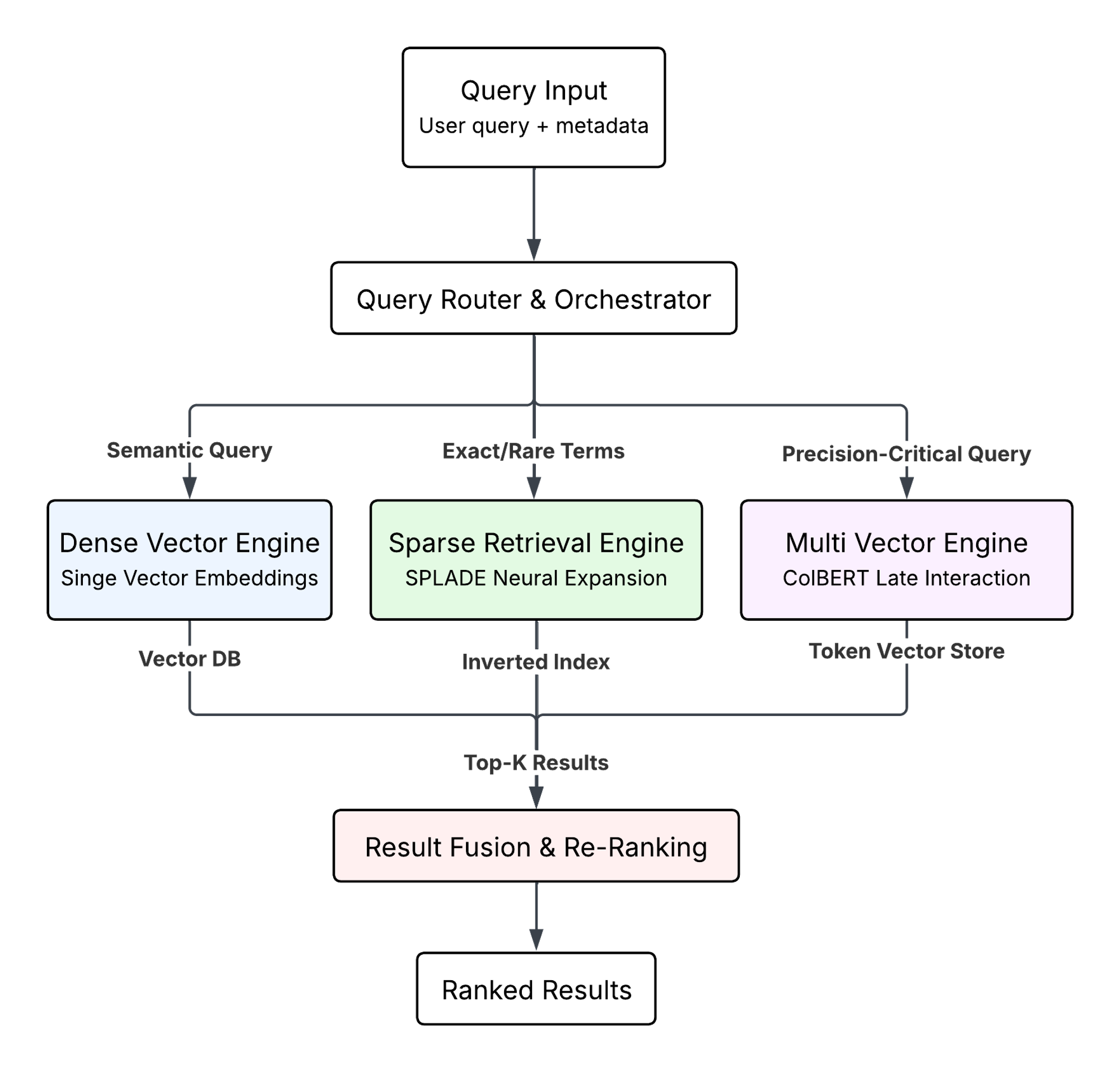
Our approach combines dense embeddings for semantic recall with sparse methods for exact matching and multi-vector representations where precision requirements justify the overhead. The infrastructure ecosystem lags behind, as most vector databases optimize exclusively for dense retrieval, requiring some custom routing logic to direct queries to appropriate retrieval mechanisms.

We build such that maximum retrieval quality comes from matching representation type to query characteristics, not from waiting for a universal embedding model that solves all cases. And when that next paradigm shift happens, we'll be ready to integrate.

Conclusion: Maturity Is Not Failure

The slowdown in fundamental embedding innovation stems from approaching mathematical limits of the single-vector paradigm, not lack of research activity. Sign-rank constraints, dimensional collapse, and scaling laws aren't engineering challenges—they're geometric impossibilities.

In other words, no amount of clever training or bigger models can overcome them.

The future lies in escaping single-vector constraints entirely: multi-vector representations like ColBERT, hybrid sparse-dense pipelines, and multimodal unification. For now, hybrid architectures offer the most practical path to maximum retrieval quality while infrastructure catches up.